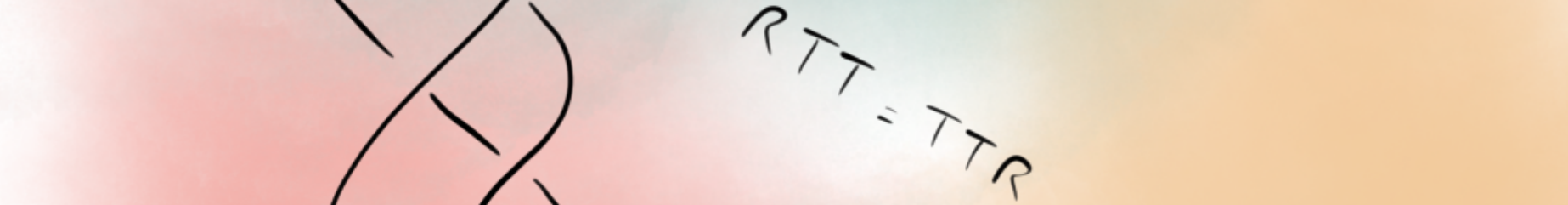Student Workshop Integrability 2023

In this talk, we are interested in an integrable spin-1 XYZ chain with twisted boundary conditions. We show that the XYZ Hamiltonian possesses the remarkably simple eigenvalue E=0. In some regime, it is conjectured to be the ground-state eigenvalue. Moreover, we express a sum rule involving the zero-energy states in terms of special polynomials. These polynomials have connections to other problems in integrable systems and enumerative combinatorics. To obtain our results, we follow an idea of Baxter's, and consider a related eighteen-vertex SOS model. There, computations are performed using Sklyanin's quantum Separation of Variables. This talk is based on joint work with Christian Hagendorf.