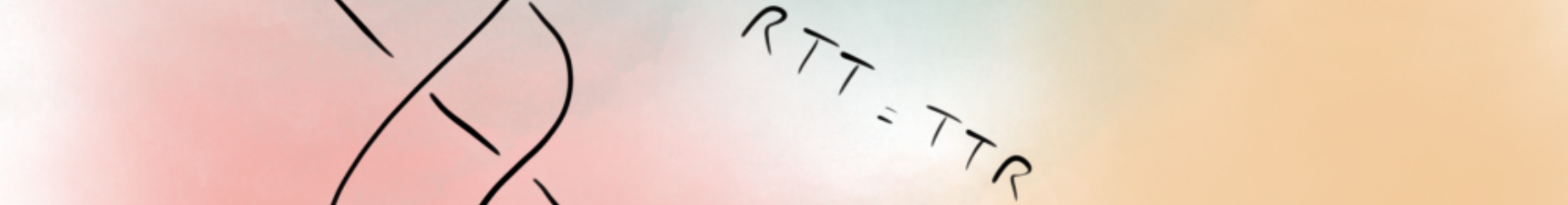Speaker
Description
In this talk, we will discuss a large class of Interaction-Round-a-Face (IRF) solvable lattice models that are based on the symmetry algebras of WZW models, namely, the affine Lie algebras $\hat{\mathfrak{su}}(n)$, $\hat{\mathfrak{ so}}(2n+1)$, $\hat{\mathfrak{sp}}(n)$, $\hat{\mathfrak{so}}(2n)$, and $\hat{G}_2$ (studied by Jimbo et al., and Kuniba, respectively). We have derived a general formula for the so-called crossing multipliers of these models and have shown (in a published paper), that these crossing multipliers can be expressed using the principally specialized characters of the algebras in question. Based on this result, we will argue that the crossing multipliers in a large class of solvable IRF lattice models can be obtained from the characters of the conformal field theory on which they are based and will discuss the relevance of this idea in the computation of the Local State Probabilities. We will also explain the generalization (this is part of a work in progress) of these models to certain quotients of the original groups. In particular, we will talk about the $SU(3)/\mathbb{Z}_3$ quotient.