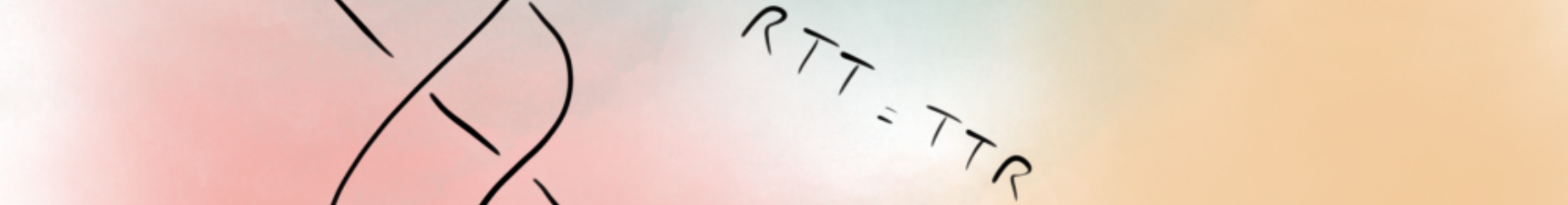Speaker
Description
We study reduced density matrices of the integrable critical RSOS
model in a particular topological sector containing the ground state.
Similar as in the spin-$1/2$ Heisenberg model correlation functions of this model on
short segments can be `factorized': they are completely determined by
a single nearest-neighbour two-point function $\omega$ capturing the
dependence on the system size and the state of the system and a set of
structure functions. The latter can be expressed in terms of the
possible operators on the segment, in the present case representations
of the Temperley-Lieb algebra $\text{TL}_n$, and are independent of the model
parameters. We present explicit results for the function $\omega$ in
the infinite system ground state of the model and compute multi-point
local height probabilities for up to four adjacent sites for the RSOS
model and the related three-point correlation functions of non-Abelian
$su(2)_k$ anyons.